LeetCode 208. Implement Trie (Prefix Tree) 前缀树实现
Description
Implement a trie with
insert,search, andstartsWithmethods.Note: You may assume that all inputs are consist of lowercase letters
a-z.
Solution
题意:实现前缀树的insert, search, and startsWith方法。
Trie的应用 Application:
前缀树(Trie 或 prefix tree)是一种树形数据结构,用来检索字符串数据集中的键key。这种高效的数据结构有广泛的应用,如:Autocomplete搜索框下的提示栏、Spell checker拼写检查器、IP routing (Longest prefix matching)IP路由中的最长前缀匹配、T9 predictive text9键预测输入、Solving word games - Boggle尝试通过修剪搜索空间来有效解决Boggle问题。
还有其他的一些数据结构用来从字符串数据集中检索某个单词word,如平衡树(balanced tree)和哈希表(hash table)。那为何还需要前缀树(Trie)呢?虽然哈希表在搜索一个键key时只需要$O(1)$的时间复杂度,但它在以下的操作中效率不高:
- 查找具有公共前缀的所有键key (Finding all keys with a common prefix);
- 以字典顺序枚举一个字符串数据集 (Enumerating a dataset of strings in lexicographical order)。
Trie优于哈希表的另一个原因在于,当哈希表大小增加时,会产生很多哈希碰撞,进而使搜索的时间复杂度恶化到$O(n)$,n是插入键key的数量。当存储许多相同前缀的键key时,Trie相比哈希表使用更少的空间。在这种情况下,Trie消耗O(m)的时间复杂度,m是key的长度。在平衡树中搜索一个键key的时间复杂度是$O(mlogn)$,
1. 节点结构 Trie node structure
Trie是一个有根的树。它的节点包含以下成员:
- 最大的连接links(孩子)的数量$R$,每一个连接link对应数据集字母表中的一个字符值。本文假设$R$是26,即小写拉丁字母的个数。
- 布尔字段 Boolean,指该节点是否对应于键key的结尾,否则仅仅是一个键key的前缀prefix。
TrieNode结构如下 (Java):
class TrieNode {
// R links to node children
private TrieNode[] links;
private final int R = 26;
// true: the node corresponds to the end of the key; false: just a key prefix.
private boolean isEnd;
public TrieNode() {
links = new TrieNode[R];
}
public boolean containsKey(char ch) {
return links[ch -'a'] != null;
}
public TrieNode get(char ch) {
return links[ch -'a'];
}
public void put(char ch, TrieNode node) {
links[ch -'a'] = node;
}
public void setEnd() {
isEnd = true;
}
public boolean isEnd() {
return isEnd;
}
}
Trie数据结构中最常用的操作是插入(insertion)和搜索(search)一个键key.
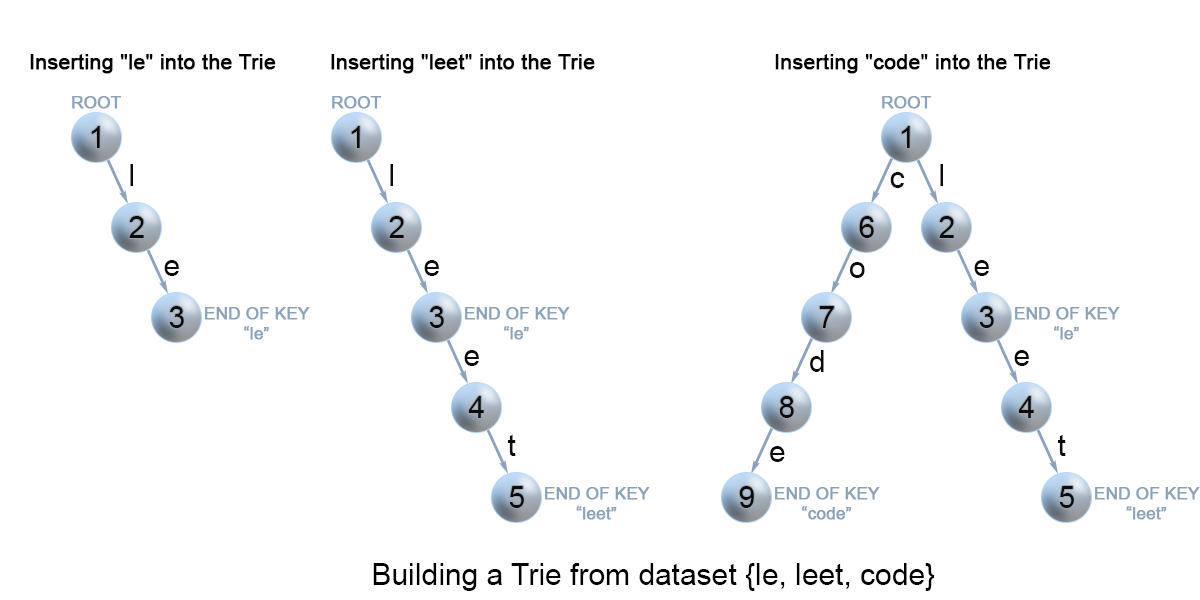
2. 插入一个键key(Insertion of a key to a trie)
需要通过搜索完成向Trie中插入一个键key。我们从Trie的根节点开始,查找Key的第一个字符来搜索一个link(孩子)。有以下两种情况:
- 该link存在,则转移到下一级孩子节点,继续搜索key的下一个字符;
- 该link不存在,则新建一个节点,用当前key的字符作为link匹配,链接为当前结点的孩子节点。
重复以上搜索匹配的步骤,直到该键key的最后一个字符,标记当前的节点为end node,算法结束。
代码如下(Java):
class Trie {
private TrieNode root;
public Trie() {
root = new TrieNode();
}
// Inserts a word into the trie.
public void insert(String word) {
TrieNode node = root;
for (int i = 0; i < word.length(); i++) {
char currentChar = word.charAt(i);
if (!node.containsKey(currentChar)) {
node.put(currentChar, new TrieNode());
}
node = node.get(currentChar);
}
node.setEnd();
}
}
Complexity Analysis
Time complexity : $O(m)$, where m is the key length. In each iteration of the algorithm, we either examine or create a node in the trie till we reach the end of the key. This takes only $m$ operations.
Space complexity : $O(m)$. In the worst case newly inserted key doesn’t share a prefix with the the keys already inserted in the trie. We have to add $m$ new nodes, which takes us $O(m)$ space.
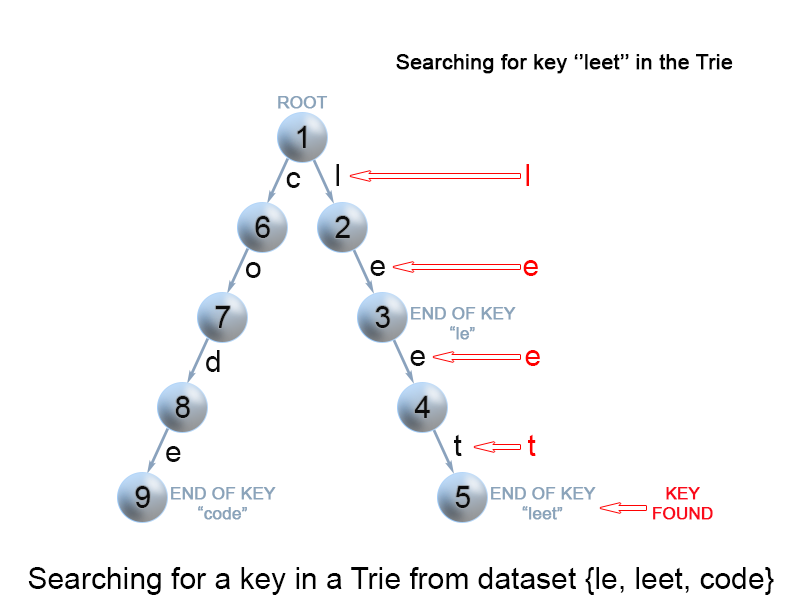
3. 搜索一个键key(Search for a key in a trie)
每个键key在Trie中表示为从根到内部节点或叶子的路径。本操作仍然从根节点及第一个key的字符开始搜索。检查当前节点是否存在此key字符的link,有以下两种情况:
- 该link存在,则转移到下一级孩子节点,继续搜索key的下一个字符;
- 该link不存在,如果没有可用的key字符,并且当前节点被标记为isEnd,则返回true;否则可能有两种情况都会返回false:
- 还剩余一些键key字符,但是不可能沿着该节点路径走下去,the key is missing;
- 没有剩余键key字符,但当前节点没有标记为isEnd。此时,当前搜索的键key只是Trie中另一个键key的前缀。
代码如下(Java):
class Trie {
private TrieNode root;
public Trie() {
root = new TrieNode();
}
// Inserts a word into the trie.
public void insert(String word) {
TrieNode node = root;
for (int i = 0; i < word.length(); i++) {
char currentChar = word.charAt(i);
if (!node.containsKey(currentChar)) {
node.put(currentChar, new TrieNode());
}
node = node.get(currentChar);
}
node.setEnd();
}
// search a prefix or whole key in trie and
// returns the node where search ends
private TrieNode searchPrefix(String word) {
TrieNode node = root;
for (int i = 0; i < word.length(); i++) {
char curLetter = word.charAt(i);
if (node.containsKey(curLetter)) {
node = node.get(curLetter);
} else {
return null;
}
}
return node;
}
// Returns if the word is in the trie.
public boolean search(String word) {
TrieNode node = searchPrefix(word);
return node != null && node.isEnd();
}
}
Complexity Analysis
Time complexity : $O(m)$, where m is the key length. In each step of the algorithm we search for the next key character. In the worst case the algorithm performs $m$ operations.
Space complexity : $O(1)$.
4. 搜索前缀key(Search for a key prefix in a trie)
搜索一个key是否是Trie中的前缀,只需要在上述的search方法基础上修改成startWith,判断返回时不用 node.isEnd() 的条件即可。
class Trie {
···
// Returns if there is any word in the trie
// that starts with the given prefix.
public boolean startsWith(String prefix) {
TrieNode node = searchPrefix(prefix);
return node != null;
}
}
Complexity Analysis
Time complexity : $O(m)$.
Space complexity : $O(1)$.